Generating Minesweeper boards in Python

Some of you might be familiar with Minesweeper from when it came bundled with Windows back in the 90s along with other games like Tetris, Taipei, FreeCell and some others in the Microsft Entertainment Pack.

Minesweeper is a single-player puzzle game where you start with a rectangular grid of squares that are all covered.

You start off knowing number of mines that are hidden in the board, but not much else.

And the object of the game is to uncover squares and avoid uncovering any squares that contain mines.

Minesweeper in Python

In the next couple of posts we are going to play Minesweeper in Python.

The first thing we need is a board, so in this post we will write code to generate random Minesweeper boards.

Then in the next post we will actually play the game.

How to play Minesweeper

First, let's talk about how things work.

To play the game, you click on a square to uncover it, revealing either:

1. A number indicating how many adjacent squares contain a mine - the number will be between 0 and 8.
2. A mine.

You start off knowing how many mines there are, but the object of the game is to figure out where the mines are, so you can avoid uncovering them.

If you uncover a mine, it explodes and you lose the game.

You win the game when you uncover all squares except for the mines.

You can flag the squares that you think are mines to keep track of them.

Note: when you flag a square, the game does not notify you if you've correctly identified a mine. It's just for your own bookkeeping purposes.

Strategy

The game strategy revolves around using the numbered squares to try to figure out where the mines are located.

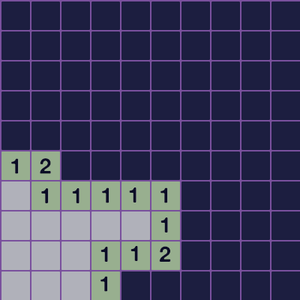
If the square's number is zero, indicating that no adjacent squares contain mines, it will either display a 0 or just be blank, depending on the version of the game you're playing.

If you uncover a zero, the game will continue to uncover adjacent squares until you end up with a perimeter of non-zero numbered squares.

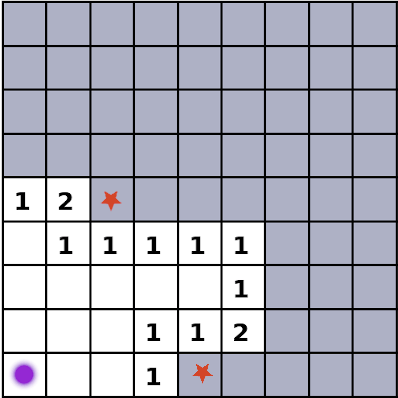
So then you can go around that perimeter and see if you can identify any unknown squares that would definitely be mines, or definitely be safe.

Here the purple dot is the starting point, and then the two red stars are covered squares that have to be mines.

You can see that the red stars have to be mines because the 1 squares diagonal to each of them have no other adjacent neighbors that could be a mine except for the one covered square, so therefore, that square must be a mine.

If there is a square that is obviously not a mine, then it can be safely uncovered.

The game continues, and in some games you will be able to win just by using this strategy.

In more difficult games, there may be an element of guessing involved, when you are left with squares that could equally likely be mines or safe squares.

In the next post on playing Minesweeper we will get into this more, but for now we are just going to generate the board.

Generating a random Minesweeper board

We'll create a 9 x 9 board with 10 mines.

import random

rows = 9
cols = 9
num_mines = 10

And I've imported Python's random module.

Start with a 2-D matrix of zeros

Basically what we're going to do is start off with this matrix of zeros.

board = [[0 for i in range(0,rows)] for j in range(0,cols)]

A zero would indicate that there are no mines adjacent to the square, so we start out with all squares being zeros.

Then we will figure out where the mines should go in the next step, and then update the values of adjacent squares as we place the mines.

Place the mines randomly throughout the grid

This is where the random module comes in.

We need a random set of squares in the board matrix, and we want to make sure that they are all unique.

So we can generate a list of (x,y) board coordinates, and then pick a random set of them equal to the number of mines we need.

board_coordinates = [(x, y) for x in range(0,cols) for y in range(0, rows)]
mine_coordinates = random.sample(board_coordinates, num_mines)

We need to sample without replacement which is what the random.sample function does.

So now we have a random sample of num_mines board coordinates - here it's 10 coordinates.

Next we will place them in the matrix board that we generated previously, and update the neighboring squares numbers as we go.

Number the squares around the mines so that we have a consistent board

The board is consistent when each numbered square correctly indicates the number of mines that are adjacent to it.

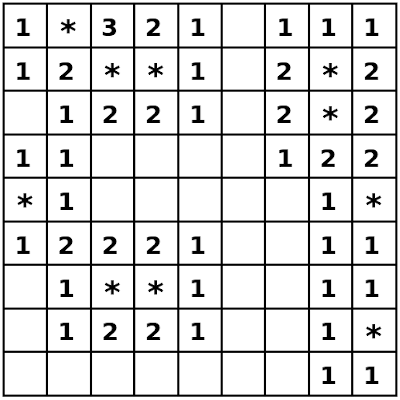
In the board, the blank squares are 0 (zero) squares, and each mine is indicated with an asterisk.

In this code I'm assigning the mines in the matrix a 9.

for mine in mine_coordinates:
    x,y = mine 
    board[x][y] = 9
    neighbors = [(x-1,y),(x-1,y+1),(x,y-1),(x+1,y-1),(x+1,y),(x+1,y+1),(x,y+1),(x-1,y-1)]
    for n in neighbors:
        if 0 <= n[0] <= cols-1 and 0 <= n[1] <= rows-1 and n not in mine_coordinates:
            board[n[0]][n[1]] += 1

Just iterate through the mine_coordinates and assign the cell at each mine coordinate in the board matrix a 9, and then look at each of its neighbors in and increment the value in that square by one, as long as it's not a mine.

This code creates a consistent Minesweeper board with randomly placed mines.

Starting the game

One reason why programmers like Minesweeper is because it is mostly a game of logic and you can use the numbered squares to figure out where the mines are.

I mentioned that in more advanced games, some guessing might be necessary, and that is also the case with the first square that you uncover in game.

When you start out with the board completely covered, you could end up uncovering a mine on your first square and losing the game immediately.

Handling the first uncovered square

Often Minesweeper games will make it so that you can't lose on your first move.

Microsoft's Minesweeper is one example. They arranged it so that if you uncover a mine on the first move, it would swap that square with another safe square, guaranteeing that your first move is always safe.

For this implementation I'm just going to update the code slightly to take the starting point out of the board coordinates, so that it doesn't get picked as a mine.

Let's say the starting point is (0,0).

starting_point = (0,0)
board_coordinates = [(x, y) for x in range(0,cols) for y in range(0, rows) if (x,y) != starting_point]

If I were making an interactive game from this, I might present the board with all covered squares, and then behind the scenes wait to generate the mines and numbers until after the user has uncovered the first square.

Testing Consistency

Now we have the finished board, and can run some tests to make sure that it is consistent, and that the constant number in each square correctly indicates the number of adjacent mines.

for i in range(0,cols):
    for j in range(0,rows):
        sq = board[i][j]
        if sq > 0 and sq < 9:
            mine_neighbors = get_mine_neighbors(i,j)
            if sq != len(mine_neighbors):
                print("not consistent!")

This code just goes through the board and for each square in the matrix, if its value is greater than zero but not 9 (a mine) then it looks at the square's neighbors to see how many mines there are.

def get_mine_neighbors(x,y):
    mines = []
    neighbors = [(x-1,y),(x-1,y+1),(x,y-1),(x+1,y-1),(x+1,y),(x+1,y+1),(x,y+1),(x-1,y-1)]
    for n in neighbors:
        if 0 <= n[0] <= cols-1 and 0 <= n[1] <= rows-1:
            if board[n[0]][n[1]] == 9:
                mines.append(n)
    return mines

The board is consistent if, for all of these numbered squares, the number of mines in the neighboring adjacent squares is the same as the current square's number.

Thanks for reading!

Stay tuned for the next post on playing Minesweeper in Python.

If you have questions or comments, feel free to write them below or reach out to me on Twitter @LVNGD.