Solving the Lowest Common Ancestor Problem in Python

Some years ago, I failed an interview problem that could be solved with a Lowest Common Ancestor(LCA) algorithm.

I was supposed to find the length of the path between two nodes in a tree, or something like that.

I started off using breadth-first search, but then after stumbling along, I sort of got lost in the tree, and never really found my way out...

My interviewer had mentioned something about a lowest common ancestor...

Lowest Common Ancestor (LCA)

• F and C => B

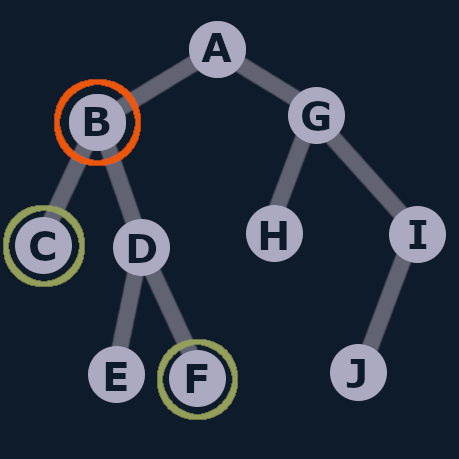
Lowest connecting node

The LCA is the lowest node that connects two nodes in the tree.

It will also be the connecting node that is closest to the root, which has a depth of zero.

In this case, it's node B.

If you look at the levels of the tree, node B has the minimum depth of the connecting nodes between F and C.

Range Minimum Query

We are going to use something called the range minimum query to solve for the LCA, which might give you a hint of what's to come.

If I'm remembering my interview question correctly, I think basically I should have:

• found the LCA of the nodes
• then add up the number of steps from each node to the LCA

Or I was supposed to return the path between them...I don't remember.

Either way...

• There are 3 steps(edges) between nodes F and C.
• F - D - B - C is the path between them.

String matching algorithms

LCA can be used for things like string pattern matching, which is useful in information retrieval problems.

Text could be stored in a suffix tree.

In a suffix tree, the leaves are all of the possible suffixes of the text.

This is useful for if you want to find all occurrences of a certain string or pattern in a text, or if you have a bunch of text documents, you might want to return all documents that contain that pattern.

Range Minimum Query

One way to find the LCA is with a range minimum query.

There are multiple ways to do this, depending on your use case.

1. First, we will flatten the tree into a list by traversing it.
2. Then we can use a range minimum query on this list to find the LCA of two nodes.

We're going to use the tree from earlier to find the LCA of the C and F nodes.

Tree: Python dictionary

First we need the tree.

tree = {'A': {'B': {'C': None, 'D':{'E': None, 'F': None}}, 'G': {'H': None, 'I': {'J': None}} } }

There are a lot of different ways to implement a tree, and here I'm just using nested Python dictionaries.

• The keys are the node names.
• Children of nodes are represented as another dictionary, nested under their parent.
• A leaf node has no children, and so its value will be None.

Traverse the tree

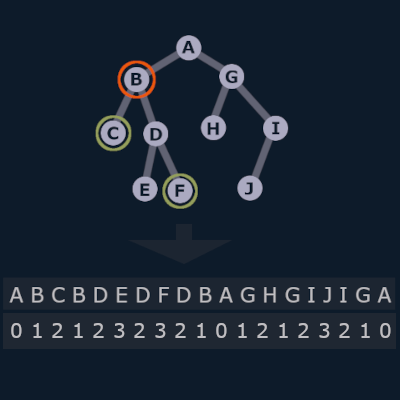
Now we're going to traverse the tree in a step-wise way, as well as keep track of the depth of each node.

This is also known as the Euler tour.

Our function for this will return two items:

1. The traversal path - a list of traversal steps.
2. Depth of each node - a dictionary.

depth_dict = {'A': 0, 'B': 1, 'C': 2, 'D': 2, 'E': 3, 'F': 3, 'G': 1, 'H': 2, 'I': 2, 'J': 3}

In the graphic above, you can see the traversal path, and also the corresponding depths of each node.

+1 Property

Notice that the depths in the traversal list have something called the +1 property, where consecutive numbers differ by 1.

Backtracking algorithm

We are using a recursive backtracking algorithm, to traverse the tree and keep track of all of the steps.

def backtrack_tree(node, parent, depth, path, depth_dict):
    if not node:
        return
    for k in node.keys():
        depth_dict[k] = depth
        path.append(k)
        #add one to depth, but not updating the variable itself in the loop
        backtrack_tree(node[k], k, depth+1, path, depth_dict)
        #backtracking steps
        if parent:
            path.append(parent)
    return path, depth_dict

The function is creatively named backtrack_tree.

Let's call it!

path_solution, depth_dict = backtrack_tree(tree, None, 0, [], {})

We are passing in:

• The tree.
• A reference to its parent(None, since we are starting with the root).
• An empty list that will be filled with the traversal path.
• And an empty dict which will hold the depths of the nodes.

Parent node

We're keeping track of the parent node, because when the algorithm is walking back up the tree, from node C -> B, for example, these are the backtracking steps and we want to add them to the solution as well.

The base case of this function is when we reach a node that has no children, and its value is None.

Otherwise, we iterate through the keys of the node, append each to the path solution, and then recurse through the children.

And we keep track of the depth and only add 1 to it in the function parameters, so that it will only increase in the recursive calls.

For this tree, the traversal path solution looks like this:

['A', 'B', 'C', 'B', 'D', 'E', 'D', 'F', 'D', 'B', 'A', 'G', 'H', 'G', 'I', 'J', 'I', 'G', 'A']

With that, we are ready to use these to find the LCA of two nodes in the tree.

Find the LCA using Range Minimum Query

Now we come back to the range minimum query stuff.

First, we reduced the tree into its list of traversal steps.

['A', 'B', 'C', 'B', 'D', 'E', 'D', 'F', 'D', 'B', 'A', 'G', 'H', 'G', 'I', 'J', 'I', 'G', 'A']

The range is the interval between nodes C and F.

We want to find the node with the minimum depth in that range..

So:

• The range interval is the path between the two nodes in question.
• Query that interval for the node with the smallest depth.

Smallest depth = closest to the root = lowest common ancestor.

Range Minimum Query Solution

There are a lot of ways you could do this, and I'm mainly going for readability here.

This function takes in the two nodes, along with the path solution and depths from the tree traversal function.

def lowest_common_ancestor(n1,n2, path, depths):
    n1_locations = []
    n2_locations = []
    for i in range(len(path)):
        if path[i] == n1:
            n1_locations.append(i)
        if path[i] == n2:
            n2_locations.append(i)
    min_index = min(min(n1_locations),min(n2_locations))
    max_index = max(max(n1_locations),max(n2_locations))
    path_segment = path[min_index:max_index+1]
    interval_depth = []
    for s in path_segment:
        interval_depth.append(depths[s])
    min_interval = min(interval_depth)
    lca_result = path_segment[interval_depth.index(min_interval)]
    return lca_result

What this function does

The function mostly iterates through each item in the the path solution list, and keeps track of the locations of each node we are querying, n1 and n2, by their list indices.

Then, it:

• gets the min and max of these locations, to get the full range interval between the two nodes.
• slices the path segment from the full solution - this is the part highlighted in red in the graphic.
• iterates through the path segment and builds lists of the depths in the segment.
• and then finally gets the minimum depth from that list, and returns the corresponding node.

You could build lookup tables if you needed to be able to do fast queries.

And the Lowest Common Ancestor is...

Node B is the lowest common ancestor.

Thanks for reading!

If you want to read more about suffix trees, and LCA + RMQ, have a look at these lecture notes:

• Advanced Data Structures - CSAIL - Lecture 10
• Advanced Data Structures - CSAIL - Lecture 11