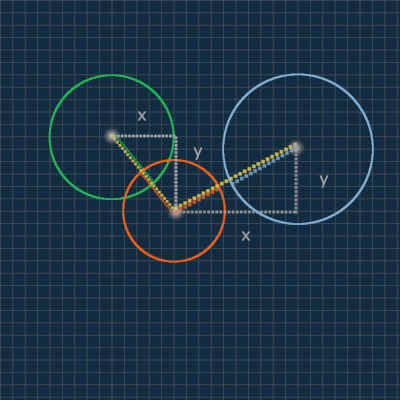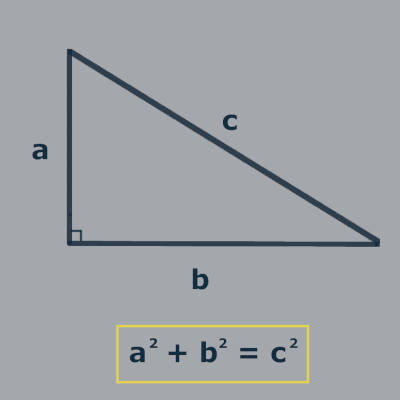Collision detection is a problem that comes up a lot in game development, and also in designing physical simulations, where the goal is to detect intersecting objects.
In D3, a force layout graph works as a physical simulation.
I'm assuming some familiarity with force layouts in D3 here - check out some of the posts in the sidebar if you're totally unfamiliar with them.
In this post we're going to adapt a built-in force in D3 that handles collision detection with circles for use with rectangles.
You might have worked with bubble charts, or a basic network graph where the nodes are circles.
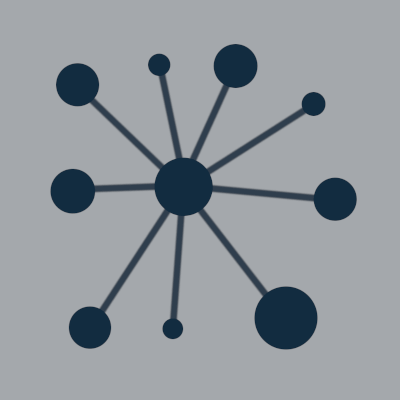
Setting up a force layout can be pretty straightforward:
Often a combination of forces work together to repel and/or attract nodes from one another to create the desired layout.
One such force works to correct overlapping nodes by detecting when two nodes are colliding and then correcting the overlap.
D3 has a built-in force for collision detection, forceCollide, which works on circles.
But what if you're working with rectangles instead of circles?
In this post we will adapt forceCollide to work on rectangles.
The new force will be called rectCollide and can be used in a simulation like:
var simulation = d3.forceSimulation()
.force('collision', rectCollide().size(function(d){return [d.width,d.height]}))
.nodes(nodes);
But let's not get ahead of ourselves quite yet.
Two basic shapes in 2-dimensional collision detection problems are circles and rectangles.
Let's have a quick overview of circle collisions.
The basic idea is to look at each pair of circles.
First draw a line between their center x-coordinates, and then a line between their center y-coordinates.
This creates a right triangle where the hypotenuse will be the distance between the two circles.
A refresher of the pythagorean theorem...
If the hypotenuse is smaller than the sum of each circle's radius, the circles must be colliding.
Compare the yellow hypotenuse for each circle pair with their radii to see how this is true.
A rectangle is described by an x and y coordinate, along with a width and a height.
We'll use the center point of the rectangle for collision detection purposes.
Instead of a radius, we will use the half-width and half-height of the rectangle, measured from the center point.
Rectangles are colliding if there is both x and y overlap.
Here we are concerned with two rectangles r1 and r2, which are colliding.
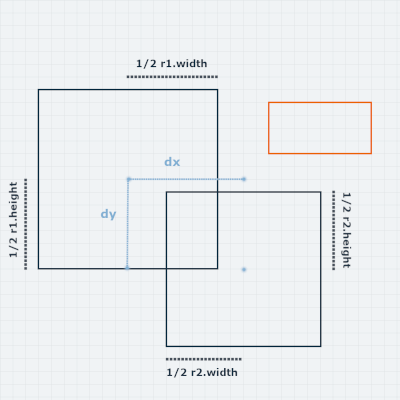
Notice that the red rectangle has y-axis overlap with r1, and x-axis overlap with r2.
But it is not colliding with anyone because if it were it would have both x and y overlap with its collision partner.
Here is pseudocode for detecting the collision between r1 and r2:
r1 = {centerX: 10, centerY: 14, , width: 14, height: 14}
r2 = {centerX: 19, centerY: 21, width: 12, height: 12}
xSize = (r1.width + r2.width)/2
ySize = (r1.height + r2.height)/2
dx = r1.centerX - r2.centerX
dy = r1.centerY - r2.centerY
absX = Math.abs(dx)
absY = Math.abs(dy)
//x overlap
xDiff = absX - xSize
//y overlap
yDiff = absY - ySize
if(xDiff < 0 and yDiff < 0){
//collision has occurred
}
Once we've detected a collision, we will respond by adjusting the velocity of the two rectangles to separate them.
To do this, we need to find the direction and speed of the collision, which we will use to adjust the velocities of the rectangles and push them apart.
If you remember your physics, velocity is a vector quantity, defined by a magnitude and a direction.
The magnitude of velocity is speed, and velocity represents an object's speed in a certain direction.
Nodes in a force layout have a velocity in both the x and y direction, with attributes vx and vy.
The separation vector will tell us a couple of things:
We will use this to calculate the collision normal, which is a unit vector that has a magnitude of 1 and gives us the collision direction.
Initialize the vector components.
sx = xSize - absX; sy = ySize - absY;
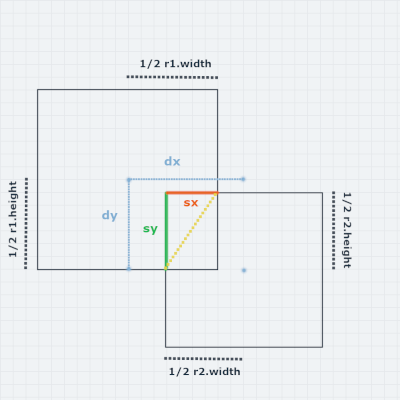
In the example collision, you can see that there is less overlap on the x-axis than on the y-axis, so the rectangles will be pushed apart along the x axis until they are separated, which will also resolve the overlap on the y-axis.
The initial separation vector is:
sx = 4 sy = 6
Then do the rest of the calculations.
if(sx < sy){
//x overlap is smaller than y overlap
if(sx > 0){
//only going to worry about x velocity, so set sy to zero
sy = 0;
}
}else{
//y overlap is smaller than x overlap
if(sy > 0){
//only going to worry about y velocity, so set sx to zero
sx = 0;
}
}
if (dx < 0){
//change sign of sx
sx = -sx;
}
if(dy < 0){
//change sign of sy
sy = -sy;
}
And the final separation vector is:
sx = -4 sy = 0
To get the collision normal, we divide the separation vector components by the distance, which is the hypotenuse of the triangle created by them - the yellow line in the graphic.
distance = Math.sqrt(sx*sx + sy*sy)
Notice that sy was previously set to zero, since the x-axis has the smallest overlap and we are therefore ignoring the y-axis, so here it breaks down to finding the square root of sx squared, which is just (the absolute value of) sx.
distance: 4
Now to get the collision normal, just divide each component of the separation vector by the distance.
collisionNormalX = sx/distance = -4/4 = -1 collisionNormalY = sy/distance = 0/4 = 0
The collision normal vector is [-1,0].
In general, the collision normal for each direction would be:
Next calculate the relative velocity of the rectangles.
We will calculate the speed of the collision from the relative velocity and the collision normal.
rVelocityX = r1.vx - r2.vx rVelocityY = r1.vy -r2.vy
Simply subtract r2's velocity from r1, for each component vx and vy.
The relative velocity and the collision normal are both vectors.
We can take the dot product of these two vectors to get the speed of the collision.
speed = rVelocityX * collisionNormalX + rVelocityY * collisionNormalY
If the speed is positive, that means the rectangles are moving towards each other, so we will need to resolve the collision.
A negative speed means they're moving away from each other and the collision will resolve itself.
We want to take the rectangle mass into consideration, so that rectangles with smaller mass are pushed more than rectangles with larger mass.
Calculate the impulse which is then used to calculate momentum, which is the product of mass and velocity.
impulse = 2*speed / (r1.mass + r2.mass);
Then use this to update the velocity of each rectangle - remember that we're only pushing the rectangles apart along the one axis with the least amount of overlap, so we only need to update one component of the velocity.
In this example it's the x-axis velocity, so we will update the vx attribute for each rectangle.
r2.vx -= (impulse * r1.mass * collisionNormalX) r1.vx += (impulse * r2.mass * collisionNormalX)
This will push the rectangles away from each other.
If you're interested in learning more about the physics of collisions, this Khan Academy article is a good starting point.
We've covered detecting and responding to a collision between two objects.
But in a D3 simulation we need to expand this to check for collisions between all object pairs.
One brute-force solution would be to use nested loops to compare all objects to all others, but that would be very slow.
forceCollide uses quadtrees to search for colliding node pairs in a much more efficient way.
A quadtree is a data structure that is used to partition a 2-D space by dividing it recursively into 4 regions.
If you're familiar with binary trees where each node has two children, in a quadtree each node has up to 4 children.
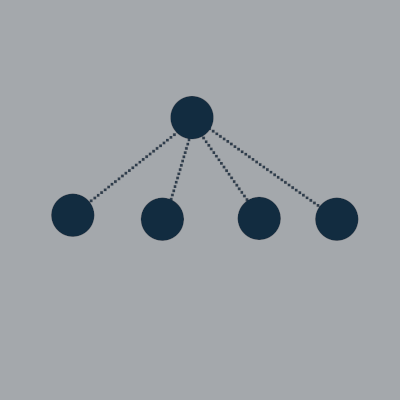
In a quadtree, each node is either a rectangle or a point, and will have up to 4 children that are rectangles and/or points.
The points are the leaf nodes, meaning they have no children.
We can efficiently determine if two nodes might be colliding by checking to see if they are located in the same quadrant in the quadtree, and continuing to traverse the tree until either:
So if we are looking at a pair of nodes where one is located in the top left quadrant, and the other is in the bottom right, then we can immediately dismiss them since they are not located near each other to begin with and definitely are not colliding.
If the two nodes are somewhat close, maybe they are both located in the top left quadrant, then we continue to traverse down until they are not in the same rectangle.
Or if we get all the way to the leaf nodes(the points), then we check to see if they are colliding with the calculations from earlier.
My physics is pretty rusty (and to be completely honest, it was not one of my best subjects in school to begin with...) so I used a few sources to work out the calculations in this post.
The main sources I used were:
For more about quadtrees, check out this interactive visualization.
Reach out below or on Twitter @LVNGD with any questions or comments!
Starting out with general purpose computing on the GPU, we are going to write a WebGPU compute shader to compute Morton Codes from an array of 3-D coordinates. This is the first step to detecting collisions between pairs of points.
Read More
In this post, I am dipping my toes into the world of compute shaders in WebGPU. This is the first of a series on building a particle simulation with collision detection using the GPU.
Read More
Finding the Lowest Common Ancestor of a pair of nodes in a tree can be helpful in a variety of problems in areas such as information retrieval, where it is used with suffix trees for string matching. Read on for the basics of this in Python.
Read More
